File & Folder Creation with File Sorting in Powershell

Long post today. Definitely my most complex and longest script. Basically what this does it is looks at two separate CSV files, one has a list of locations and the other has a list of users/ people with a location assigned to them as well as some other attributes. WARNING! this script is variables center!

First of all, lets import our locations and create a folder with that location name. This is the code I used for this:

$get_Location_csv = Import-Csv -path 'C:\#PATH TO LOCATIONS CSV FILE'
[string]$root_dir = 'C:\#PATH TO ROOT FOLDER'
try{
 foreach ($location_data in $get_Location_csv){
  $location = $location_data.location #obtain location info
  if(Test-Path -Path $root_dir$location){
   Write-Host "Path already exists!"
  }else{
   New-Item -path $root_dir -Name "$location" -ItemType directory -ErrorAction SilentlyContinue
  }
 }

So from this you can see that we import the folder with the CSV values, check if where the folder will be created already exists, if so then output text, if not then create the folder with the location name. In case you were wondering, here is the value from my CSV file for the locations:

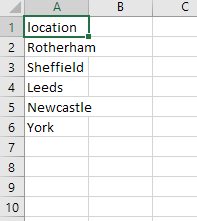
Now that the files have been created, we want to import the other CSV file which contains a list of the users we need sorting and where they need sorting to. Below is the code I used to get the values I wanted, create the file, name it, put data in it and then put it into the relevant folder based on the users location.

$get_user_data = Import-Csv -Path "$root_dir\#USER INFO CSV"

foreach ($i in $get_user_data){
 $first = $i.first
 $last = $i.last
 $username = $i.username
 $location = $i.location
 $datetime = [datetime] (Get-Date)
 $district = $i.district
 foreach($l in $location){
  New-Item -Path "$root_dir$location" -Value "$first $last $location District = $district $datetime" -Name "$username .txt" -ErrorAction Stop
 }
}

To end the code off so that it worked more cleanly in the case of an error I added the following:

}catch{
 $_.exception.message
 Write-Warning 'location:'$i 'was not created successfull!'
}

This catches any errors that might occur during the scripts operation

Again, in case your wondering what is actually in the users CSV file, you can see that in the below screenshot:

 

This is the output of the script

Here you can see the folders the script created:You can see that the script created all of the locations in the location CSV file. (Leeds, Newcastle, Rotherham, Sheffield, York)

Here you can see the files that are in one of the folders (I chose Leeds):

Here is what is in each of the files:

From these screenshots you can see that the script has successfully created and sorted the files by the location defined to each user in the users CSV file. You could probably make this work from just the one CSV file, but I went for the long way round 🙂

Here is the entire script!

$get_Location_csv = Import-Csv -path 'C:\#PATH TO LOCATIONS CSV FILE'
[string]$root_dir = 'C:\#PATH TO ROOT DIRECTORY'
try{
 foreach ($location_data in $get_Location_csv){
  $location = $location_data.location
  if(Test-Path -Path $root_dir$location){
   Write-Host "Path already exists!"
  }else{
   New-Item -path $root_dir -Name "$location" -ItemType directory -ErrorAction SilentlyContinue
  }
 }

$get_user_data = Import-Csv -Path "$root_dir\Users.csv"

foreach ($i in $get_user_data){
 $first = $i.first
 $last = $i.last
 $username = $i.username
 $location = $i.location
 $datetime = [datetime] (Get-Date)
 $district = $i.district
 foreach($l in $location){
  New-Item -Path "$root_dir$location" -Value "$first $last $location District = $district $datetime" -Name "$username .txt" -ErrorAction Stop
 }
}
}catch{
 $_.exception.message
 Write-Warning 'location:'$i 'was not created successfull!'
}